4.6.2 Vom Ortsraum zum Frequenzraum
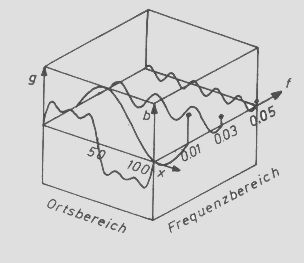
Ein Bild wird vom Ortsraum in den Frequenzraum überführt,
indem man eine mathematische Operation anwendet, bekannt als Fourier-Transfomation.
Dabei wird eine kontinuierliche Funktion durch die Grauwerte gelegt. Diese
Kurve wiederum kann durch eine unendliche Summe von Sinus- und Cosinusfunktionen
dargestellt werden mit verschiedenen Amplituden, Frequenzen und Phasen.
Zur Veranschaulichung betrachten wir es im eindimensionalen
Raum (siehe Abb. rechts, linkes Bild):
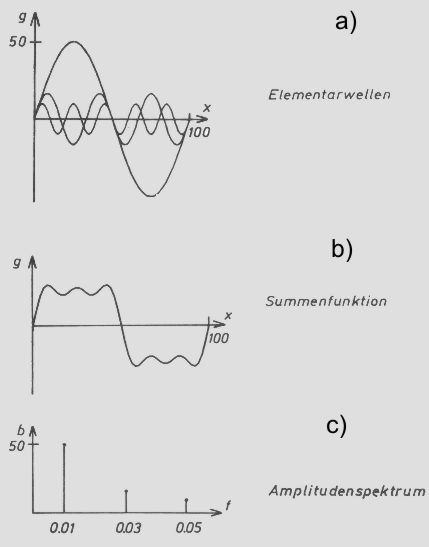
Funktion g(x) ist eine eindimensionale Grauwertfunktion. Sie zeigt eine komplexe
Wellenform (Abb b), die z.B. eine Zeile eines Bildes beschreibt. Abb
a zeigt, wie diese Funktion in mehrere Sinus- und Cosinus-Wellen zerlegt
werden kann mit verschiedenen Frequenzen. Sie setzt sich aus den 3 Elementarwellen
mit den Frequenzen 0.01, 0.03 und 0.05 zusammen. Als Amplitudenspektrum (Abb
c) bezeichnet man die Amplituden der Elementarwellen, die über den
Frequenzen 0.01, 0.03 und 0.05 aufgetragen werden.
[Kraus 1990] 