|
|
Dies ist die Darstellung einer multidimensionalen Normalverteilung. In der
Statistik wird sie oft verwendet, da ihre mathematische Handhabung nicht zu
komplex ist und sie außerdem die Natur näherungsweise oft gut beschreibt.
Die Normalverteilung für 1D ist die Gauß'sche Normalverteilung: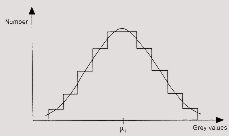
Normalverteilung (Gauß'sche Funktion)
[Bähr, Vögtle 1999]
Da wie schon erwähnt, jede Klasse eine eigene spezifische Verteilung
hat, hat die Gauß'sche Funktion jeder dieser Klassen verschiedene Mittelwerte
und Varianzen 
.
Bei 2D haben die Verteilungen die Form von Ellipsen.
- Mittelwert = Mittelpunkt des Ellipsen
- Varianz = Form und Orientierung der Ellipsen
Bei mehrkanaligen Verteilung erhält man statt der einfachen
Varianz s die Kovarianzmatrix
C
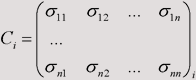
Für eine multispektrale Klassifizierung brauchen wir die realen Werte der Klassen, d.h. die unbekannten Parameter der Normalverteilung (Mittelwert µ und Kovarianzmatrix C). Diese Unbekannten werden über Probenflächen bestimmt, die "Trainingsgebiete".
Das Resultat einer Klassifizierung hängt in großem Maße davon ab, wie sehr diese mathematischen Verteilungsfunktionen der Klassen der "wirklichen" Verteilung in der Natur entsprechen. Die Grundfrage ist dabei natürlich: "Wie korrekt lässt sich die Natur in Klassen unterteilen, die der Normalverteilung folgen?"
| Home > Lernmodule > Modul 6 |