Home > Lernmodule > Modul 10

 

2.3.2 Netze

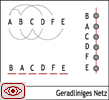
Die graphische Darstellung ist ein Netz (s. dazu 2.2.4 Darstellung der Ebene), wenn die Beziehungen in der Ebene zwischen allen Elementen ein und derselben Komponente zum Ausdruck kommen.
Das Netz wird konstruiert, indem zuerst alle Beziehungen provisorisch erstellt werden. Im Anschluss daran wird die einfachste und prägnanteste Darstellung ermittelt. Dieses Konstruktionsprinzip unterscheidet das Netz vom Diagramm.
Netze bieten die Möglichkeit der schnellen Transkription verbaler Informationen in einem graphischen Bild durch die beiden Dimensionen der Ebene. Solche Konstruktionen ermöglichen ein erstes Ordnen und Betrachten der Struktur des Beziehungssystems, wobei möglicherweise eine aus dieser Struktur abgeleitete, einfachere Konstruktion (Transformation) erstellt werden kann.
Treten drei oder mehr Komponenten auf, so werden die Farb-Muster-Variablen genutzt.

Die Implantation verfügt über drei elementare Grundfiguren: Punkt, Linie und Fläche. Die Imposition beschreibt die Gliederung dieser Figuren (rechtwinklig oder kreisförmig) sowie das Bilden eines geordneten Feldes. Das Stereogramm kann zudem Raumtiefe vermitteln und ein Netz im dreidimensionalen Raum entstehen lassen.

Durch die Kombination von Implanation und Imposition lassen sich weitere Netze konstruieren.

Die prägnanteste Darstellung eines Netzes ist die mit der geringsten Anzahl von bedeutungstragenden Schnittpunkten. Bei nicht allzu komplexen Informationen haben sich Kreis-Konstruktionen als beste visuelle Lösung herausgestellt. Ist die Information jedoch sehr komplex, so bietet sich eine graphische Matrix zur Vereinfachung der Darstellung an.